運とは「ランダムなもの、つまり法則なしに起こるもの」を指します。
ある出来事の背後にある方法やパターンがなければそれはランダム。つまり予測することは不可能です。
では、運の逆ってなんでしょうか?それはスキルです。つまり知識や能力を使って実際に結果に影響を与えることができるものです。 ベッティングを攻略するには基本的に、スキルと運の割合がどのくらいあるかを考え、そのうえでスキルが有効だと判断した場合は、選手やイベントの属性をきちんと評価(またの名をハンディキャップ)したうえでベットを決める。これが必勝法です。
コイントスもサイコロの目も完全にランダムです。だからこそあらゆるスポーツでどちらがキックオフするのか、どちらがサーブ権を持つのかなどを決める最適な方法として使われています。 コインやサイコロには記憶がないため、1回のトスやサイコロの出た目が次投げる際に影響することは全くありません。 このようなものにベットするのも楽しいですが、戦略的なアプローチはできないので、単発でランダムなイベントに対してベットして勝ったときは、スキルが関与していないのでこれがいわゆる「ラッキー」ってことになります。
運の割合を測るには
コイントス1回の結果は完全ランダムですが、何回も繰り返しやる長期的な確率はランダムではありません。その理由は、結果の確率は計算が可能で、連続するランダムな事象はベル曲線と呼ばれる法則(大数の法則とも言います)に従っているからです。
「P値」と呼ばれるランダムな事象の起こりえる結果の確率を示す値で、物事にどのくらい相互関係があるかを測ることができます。しかしこれは、かなり抽象的でわかりづらいです。 ある出来事に運がどの程度影響するかを理解するには、運とスキルに値を割り振り、サンプルが増えるにつれてそれらがどのように作用するかを見る必要があります。
「2つの瓶」理論
2つの瓶にボールが詰められていたとします。 1つ目の瓶は「運」でもうひとつが「スキル」とします。 スキルの瓶に入るボールは、0(スキルゼロ)、プラス1またはプラス2の3種。 もう一つの「運」の瓶は、マイナス3(大凶)、0(ついてない)、プラス3(ついてる)の3種。 そして、それぞれの瓶から同じ数のボールを引き、その点数を合計します。0点以上のスコアはポジティブな結果を意味します。

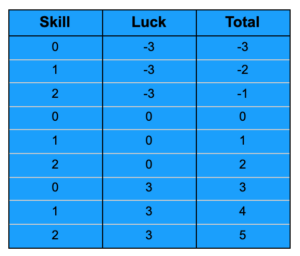
この表は一つの瓶で起こりえる結果を示しています。ここでは、ポジティブな結果の範囲がネガティブな結果を上回っていますが、たとえ高いスキルがその頻度で存在したとしても、極端に悪い運でネガティブになることもあります。 (より深い考察はJoseph Buchdahl著の「Squares & Sharps, Suckers & Sharks」を読むことをおすすめします。)
この例えはシンプルなものですが、各瓶からボールを繰り返し引いていくと、スキルの要素が運よりも大きい、つまり非ランダムな事象においては、繰り返すうちにスキルの影響が次第に大きくなることを示しています。 スポーツ競技の一般的な形式(ゲーム数やセット数など)や、大逆転がどれだけ起こりえるかを考えれば、わかりやすいと思います。
「2つの瓶」理論をスポーツベッティングに当てはめると・・・
スポーツ競技は基本的に、よりスキルを持ったパフォーマーが「頂点に立つ」ことができるように構成されています。 スヌーカーの世界選手権から、テニスのメジャー大会やUFCの王座決定戦まで、ラウンドが進むにつれて、あるいはステータスの高い競技では、運ではなくスキルが重要な要素となるように、つまり何度も繰り返した末に結果が決まる仕組みになっているんです。
テニスの例
テニスを例にとると、スキルが運よりも大きな要素であることは明らかですが、ラインの判定や、天候の影響、ネットからのボールの落下地点など、少なからず運はやっぱり存在します。 スキルの劣る選手がリスクの高いパッシングショットを多く打ってみたり、セカンドサーブを速くしてみるなどのときには、運も一役買うといえるでしょう。
先ほどの瓶の例と同じように、スキルという要素が大きいものの、運も存在するスポーツにおいて、それぞれの割合は、(オッズに基づいて)運/スキルどちらを優先するかによってきます。スポーツの試合におけるポイントはそれの繰り返しにすぎないのです。 しかし、ボールを1つずつ瓶から引く(1点マッチに相当)だけで、結果が決まることはありません。1回で結果が決まるのでればそれは運が決定的な要素になります。
テニスの試合結果に対するスキルの影響度合いは、反復回数(ポイント)が増えるにつれて大きくなります。雑誌Significanceの2015年版に掲載された記事でクリス・グレイの研究が、これをうまく説明しています。
グレイの研究
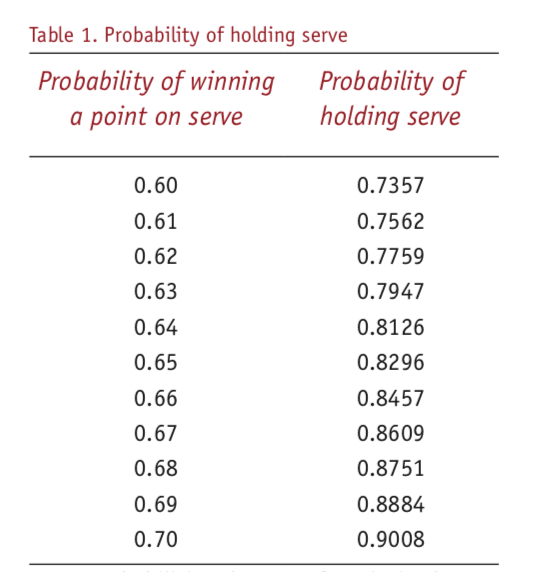
グレイは、トップ50選手のデータ(2014年)に基づき、サーブでポイントを獲得する確率(表1左)がおよそ60%~70%、 そして、サービスゲームをキープ(表1右)する確率は73.6%~90.0%という統計を出しました。
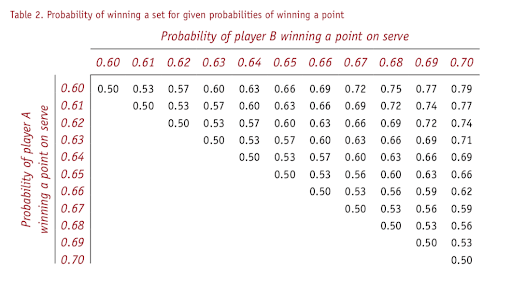
表2は選手B(横軸)、選手A(縦軸)のサーブでポイントを獲得する確率から、サービスゲーム獲得率を出したものです。どちらの選手も同レベルのスキルだった場合、どう転ぶかは明白です。
例えば、二人ともサーブでポイントを獲得する確率が0.6である場合は、サービスゲームで勝つ確率も同じで 0.5または50%です。
ここでわかることは、サービスゲームで勝つ確率はポイント獲得率の差よりも大きいことです。 これはさっきの瓶の理論から、直感的にわかることですが、試合が長引けば長引くほど、多くのサンプルが取れ、より優れた選手が勝つ確率が高くなります。
しかし、選手たちのスキルは同等であるため、運も影響することを理解することが重要で、むしろ運が2人の選手の差ということもできます。
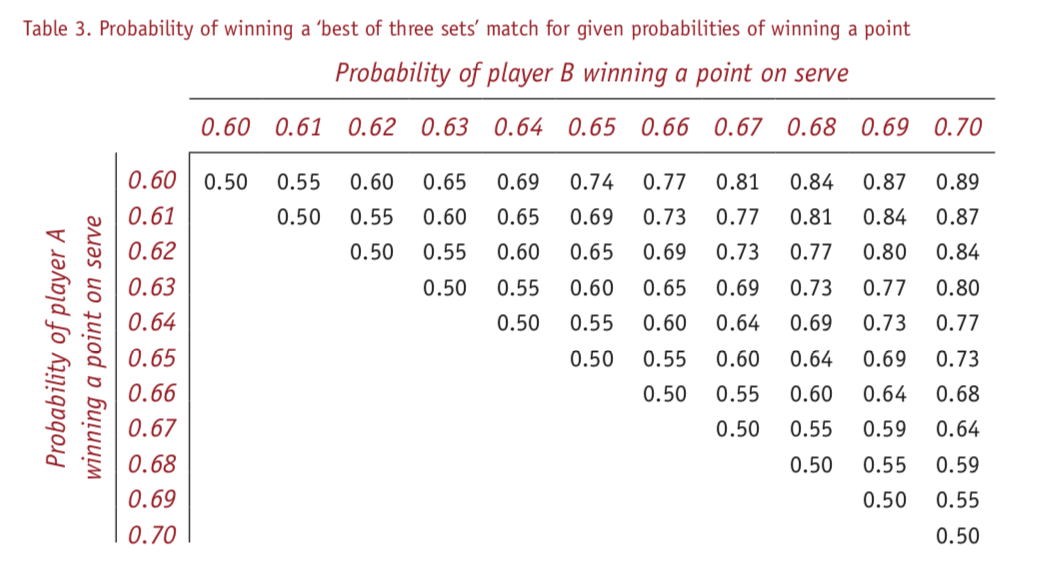
極端な例でいうと、サーブで勝つ確率が0.70のA選手と0.60のB選手という実力差がある場合だと、1セットではA選手が勝つ確率が79%ですが、ベストオブスリーセットマッチになると89%に上がります。
すでに述べたように、最も重要な大会ほど繰り返しが多くなります。テニスのグランドスラムもそうで、(男子は)ベスト3からベスト5に形式が移行しました。 グレイによると:
「サーブでポイントを獲得する確率が69%と61%の選手を考えてみよう。 これは、69%の選手が74%の確率でセットを獲得し、90%の確率で試合に勝つことを意味する。 トップ10の選手が70~100位の選手と対戦するのはよくあることだ。 このモデルとパラメーターを用いると、もし2セット負けていたとしても、大逆転のチャンスは42%あるということになる。」
まとめ
グレイが現実のデータを使って示しているのは、瓶の例えとまったく同じです。 スキルは、時間や繰り返しによって影響力を増していくのです。 ここまでの重要ポイントはこちら:
グランドスラムでは、通常のATP大会よりもフェイバリット選手(オッズで人気のある選手)が勝つことが多い、これは長い試合フォーマットになるとより実力差が際立つからです。 逆に、標準的なATPの大会やWTAの大会(ベストオブスリーセットマッチ)では予想外の展開が起こる可能性が上がります。
一度その理論を理解すれば、あらゆるスポーツに当てはめることができ、それぞれの形式によって結果のパターンを導き出すことができます。 クリケット(20/20)やスヌーカー(6red)のような、よりコンパクトな競技で予測不可能な結果が起こりえる、短い形式の競技について考えてみましょう。 特にスヌーカーは、1952年の決勝戦が145フレームだったように、長い道のりになることもあります。
この、運と繰り返しの概念を聞いたうえでウィンブルドンの近年起こった2つの壮絶な対戦を思い出すと、納得がいくかもしれません。 コート表面の高速サーブ選手への適性が高まっているため、ポイントの長さが短くなり=1ポイント内での繰り返しが減り、その結果、1ポイントあたりで運が果たす役割、つまり、非常に互角のビッグサーバー同士の対戦を、単純な消耗戦に変えてしまっているのです。 これが試合形式の変更(ベストオブスリーマッチからファイブマッチ)につながっています。
また、これを使って、運がより大きな影響力を持つような出来事や、運がゲームのパラメーターを変えるようなイベントを探してもいいと思います。 ゴルフは非常にいい例です。 選手がティーオフするタイミングは完全にランダムですが、1つのイベントで見た場合、その日の天候によって劇的な影響を与える可能性があります(これはイベント単位では重要ですが、シーズン単位では平均化されることが予想されます)。 リンクスで行われる全英オープンのように、天候が不安定な会場では特に当てはまります。
また、ゴルフ場は他のスポーツに比べて桁違いに広く、運とともに複雑な要素が相互作用する環境です。
例外はあるの?
例えば、ペナルティキックは非常に難しく、スキルと運のバランスを崩す可能性があります。 90分でうまく決着をつけるために、通常の試合時間は30%延長され、基本的に有利なチームが勝つ確率が高まりますが、それでも決着がつかない場合は、突然、運の影響がはるかに大きくなる形式に切り替わります。 その上、一回きりの試合ということを考慮しなければならず、賭け金を失いたくない気持ちが戦術に影響を及ぼし、その結果、運よりもスキルが勝るべきだという考えに歪みが生じる可能性があります。
この記事とシンプルな「2つの瓶」の例えが、スポーツにおける運の役目や、ベッティングにおける運の考え方について、より理解いただけるきっかけになっていれば幸いです。 ポイントは、結果が運よりもスキルに影響を受ける場合、その影響は時間の経過とともに大きくなることをお忘れなく。
要約 – この複雑なテーマを極簡単に一言で示すと、英語にあることわざがあげられます。「Cream rises to the top」-これは、優秀な人/ものは遅かれ早かれ頭角を表す、という意味です。
ベッティングにおける運の役割についてすべてわかったところで、スポーツブックに行って、今日学んだことをぜひ実践に移してみてください!